The Electronic configuration of helium molecule is (σ 1 s 2) (σ ∗ 1 s) 2 and hence the bond order is 0. Thus 'Zero' value indicates that Helium H e 2 molecule does not exist.that means diatomic Helium. No, helium is not a diatomic nonmetal. The key difference between monatomic and diatomic is that the monatomic species have one atom whereas the diatomic species have two.
Bond Order
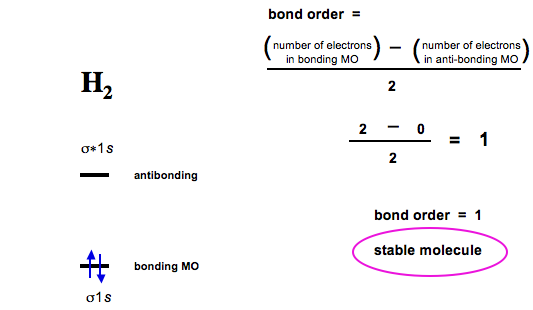
In the Lewis electron structures, the number of electron pairs holding two atoms together was called the bond order. Within the molecular orbital approach, bond order is defined as one-half the net number of bonding electrons:
[ text{bond order}=dfrac{text{number of bonding electrons} - text{number of antibonding electrons}}{2} label{9.8.1} ]
To calculate the bond order of (H_2), we know that the (σ_{1s}) (bonding) molecular orbital contains two electrons, while the ( sigma _{1s}^{star } ) (antibonding) molecular orbital is empty. The bond order of (H_2) is therefore
[ text{bond order}=dfrac{2-0}{2}=1 label{9.8.2} ]
This result corresponds to the single covalent bond; double and triple bonds contain four or six electrons, respectively, and correspond to bond orders of 2 and 3.
We can use energy-level diagrams to describe the bonding in other pairs of atoms and ions where n = 1, such as the H2+ ion, the He2+ ion, and the He2 molecule. Again, we fill the lowest-energy molecular orbitals first while being sure not to violate the Pauli principle or Hund's Rules.
Figure (PageIndex{1a}) shows the energy-level diagram for the H2+ ion, which contains two protons and only one electron. The single electron occupies the (σ_{1s}) bonding molecular orbital, giving a (σ1s)1 electron configuration. The number of electrons in an orbital is indicated by a superscript. In this case, the bond order is (via Equation ref{9.8.1})
[text{bond order}=dfrac{1-0}{2}=1/2]
Because the bond order is greater than zero, the H2+ ion should be more stable than an isolated H atom and a proton. We can therefore use a molecular orbital energy-level diagram and the calculated bond order to predict the relative stability of species such as H2+. With a bond order of only 1/2 the bond in H2+ should be weaker than in the H2 molecule, and the H–H bond should be longer. As shown in Table (PageIndex{1}), these predictions agree with the experimental data.
| Species | Electron Configuration | Bond Order | Bond Length (pm) | Bond Energy (kJ/mol) |
|---|---|---|---|---|
| H2+ | ((σ_{1s})^1) | 1/2 | 106 | 269 |
| H2 | ((σ_{1s})^2) | 1 | 74 | 436 |
| He2+ | ( left (sigma _{1s} right )^{2}left (sigma _{1s}^{star } right )^{1} ) | 1/2 | 108 | 251 |
| He2 | ( left (sigma _{1s} right )^{2}left (sigma _{1s}^{star } right )^{2} ) | 0 | 5,500 | (4.6 times 10^{−5}) |
Figure (PageIndex{1b}) is the molecular orbital energy-level diagram for (ce{He_2^{2+}}). This ion has a total of three valence electrons. Because the first two electrons completely fill the (σ_{1s}) molecular orbital, the Pauli principle states that the third electron must be in the ( sigma _{1s}^{star} ) antibonding orbital, giving a ( left (sigma _{1s} right )^{2}left (sigma _{1s}^{star } right )^{1} ) electron configuration. This electron configuration gives a bond order (via Equation ref{9.8.1}) of
[text{bond order}=dfrac{2-1}{2}=1/2]
As with H2+, the He2+ ion should be stable, but the He–He bond should be weaker and longer than in H2. In fact, the He2+ ion can be prepared, and its properties are consistent with our predictions (Table (PageIndex{1})).
Example (PageIndex{1}): The (ce{He_2^{2+}}) ion
Use a molecular orbital energy-level diagrams to predict the bond order and stability of the (ce{He_2^{2+}}) ion.
Given: chemical species
Asked for: molecular orbital energy-level diagram, bond order, and stability
Strategy:
- Combine the two He valence atomic orbitals to produce bonding and antibonding molecular orbitals. Draw the molecular orbital energy-level diagram for the system.
- Determine the total number of valence electrons in the He22+ ion. Fill the molecular orbitals in the energy-level diagram beginning with the orbital with the lowest energy. Be sure to obey the Pauli principle and Hund’s rule while doing so.
- Calculate the bond order and predict whether the species is stable.
Solution:
A Two He 1s atomic orbitals combine to give two molecular orbitals: a (σ_{1s}) bonding orbital at lower energy than the atomic orbitals and a ( sigma _{1s}^{star } ) antibonding orbital at higher energy. The bonding in any diatomic molecule with two He atoms can be described using the following molecular orbital diagram:
B The He22+ ion has only two valence electrons (two from each He atom minus two for the +2 charge). We can also view He22+ as being formed from two He+ ions, each of which has a single valence electron in the 1s atomic orbital. We can now fill the molecular orbital diagram:
The two electrons occupy the lowest-energy molecular orbital, which is the bonding ((σ_{1s})) orbital, giving a (σ1s)2 electron configuration. To avoid violating the Pauli principle, the electron spins must be paired.
C So the bond order is (via Equation ref{9.8.1})
Is Magnesium A Diatomic
[ dfrac{2-0}{2} =1 nonumber]
He22+ is therefore predicted to contain a single He–He bond. Thus it should be a stable species.
Exercise (PageIndex{1}): The (ce{H_2^{2−}}) Ion
What Is A Diatomic Molecule
Use a molecular orbital energy-level diagram to predict the valence-electron configuration and bond order of the (ce{H_2^{2−}}) ion. Is this a stable species?
Is Iron Diatomic
Helium Is Diatomic Yet
(ce{H_2^{2−}}) has a valence electron configuration of ( left (sigma _{1s} right )^{2}left (sigma _{1s}^{star } right )^{2} ) with a bond order of 0. It is therefore predicted to be unstable.
